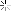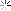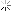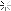Thread: problem with understanding boolean logic

In my Be Prepared Comp Sci textbook, I ran into this question:

Exercise 3

Assuming that x, y, and z are integer variables, which of the following three logical expressions are equivalent to each other, that is, have equal values for all possible values of x, y, and z?

 
    (x == y && x != z) || (x != y && x == z)
 
    (x == y || x == z) && (x != y || x != z)
 
    (x == y) != (x == z)
 
    None of the three
 
    A. I and II only
 
    B. II and III only
 
    C. I and III only
 
    D. I, II, and III

I selected B, but got it wrong. I really think I need help understanding boolean logic. The correct answer says something else but I don't get the logic. Here is the correct answer:

Answer Key
The following model answer has been provided to you by the grader. Carefully compare your answer with the one provided here.
Expression III is the key to the answer: all three expressions state the fact that exactly one out of two equalities, x == y or x == z, is true. Expression I states that either the first and not the second or the second and not the first is true. Expression II states that one of the two is true and one of the two is false. Expression III simply states that they have different values. All three boil down to the same thing. The answer is E.

In exercise 4, I get the same problem:

Exercise 4

The expression !((x <= y) && (y > 5)) is equivalent to which of the following?

 
A. (x <= y) && (y > 5)
 
B. (x <= y) || (y > 5)
 
C. (x >= y) || (y < 5)
 
D. (x > y) || (y <= 5)
 
E. (x > y) && (y <= 5)

Exercise 4
ABCDE
Incorrect
Score: 0 / 1
Submitted: 2/10/2014 8:21pm
Your answer is incorrect.
Answer Key
The following model answer has been provided to you by the grader. Carefully compare your answer with the one provided here.
The given expression is pretty long, so if you try to plug in specific numbers you may lose a lot of time. Use De Morgan's Laws instead:

 
!((x <= y) && (y > 5))
 
!(x <= y) || !(y > 5)

When ! is distributed,
&& changes into ||, and vice-versa

(x > y) || (y <= 5)

My boolean algrebra is rusty, but here goes...

For exercise 4, De Morgan's Theorem states that (using Java notation):

!(A && B) == !A || !B

If you substitute A with (x <= y), and B with (y > 5), you get:

!((x <= y) && (y > 5))
= !(x <= y) || !(y > 5), by De Morgan's Theorem

Note that the opposite of (x <= y) is (x > y). Similary, the opposite of (y > 5) is (y <= 5). Applying these opposites to the NOT expressions above,

!(x <= y) || !(y > 5)
= (x > y) || (y <= 5)

i.e., answer D.

For exercise 3,

All three boil down to the same thing. The answer is E.

What is E? The possible answers you provided above are:

    None of the three
 
    A. I and II only
 
    B. II and III only
 
    C. I and III only
 
    D. I, II, and III

My (rusty) calculations and the statement "all three boil down to the same thing" suggests that it should be D.

Originally Posted by jashburn

For exercise 3,

What is E? The possible answers you provided above are:

My (rusty) calculations and the statement "all three boil down to the same thing" suggests that it should be D.

Actually, I typed it wrong. The options are:

 
A. None of the three
 
B. I and II only
 
C. II and III only
 
D. I and III only
 
E. I, II, and III

--- Update ---

Thanks. I'm going to post another understanding question about exercise 6 soon.

Took a bit of time to type up the explanation for exercise 3 properly, but here it is.

Let:

• A be (x == y)
• B be (x == z)
• ¬A be NOT A (x != y) (and similarly ¬B be NOT B (x != z))
• A ∧ B be (A && B)
• A V B be (A || B)

For expression I,

(x == y && x != z) || (x != y && x == z)

can be rewritten as

(A ∧ ¬B) V (¬A ∧ B)

For expression II,

(x == y || x == z) && (x != y || x != z)

can be rewritten as

(A V B) ∧ (¬A V ¬B)

which can be expanded and changed using boolean algebra to:

(A ∧ ¬A) V (A ∧ ¬B) V (B ∧ ¬A) V (B ∧ ¬B)
= 0 V (A ∧ ¬B) V (B ∧ ¬A) V 0
= (A ∧ ¬B) V (¬A ∧ B)

and therefore is the same as expression I.

For expression III,

(x == y) != (x == z)

can be rewritten as

A != B

which can be interpreted as "A and not B, or not A and B" because if A is true, B must be false, and vice versa. Both A and B cannot be both true or false at the same time. As such, the expression can be rewritten as

(A ∧ ¬B) V (¬A ∧ B)

and therefore is the same as expression I. Hence all 3 expressions are equivalent.

It can be quite tricky to understand expression III, but since there are only A and B, you can put it into a truth table such as the following:

A	B	A != B
0	0	0
0	1	1
1	0	1
1	1	0

and again, you'll get

(A ∧ ¬B) V (¬A ∧ B).

Btw, as an aside, the 3 expressions represent the XOR (exclusive-OR) logic.